Scala ile dengeleri gözetelim: Bir Red-Black Tree hikayesi

11/03/2013

Binary Tree'ler özellikle değişken veri kümelerini saklamak ve arama yapmak için uygun veri yapılarıdır. Ortalama durumda binary tree arama performansı O(log n) olur. Ancak yeni veriler eklendikçe ve tree dengelenmedikçe performans düşer. En kötü durum senaryosunda binary tree bir liste gibi davranır ve arama performansı O(n) olur. Bu yazıda bu durumlardan bahsetmeye ve balanced binary tree veri yapılarından biri olan Red-Black Tree veri yapısını Scala ile gerçeklemeye çalışacağım.

Aşağıda bir binary tree örneği görülüyor. İşe önce binary tree veri yapısını Scala ile gerçekleyerek başlayalım.

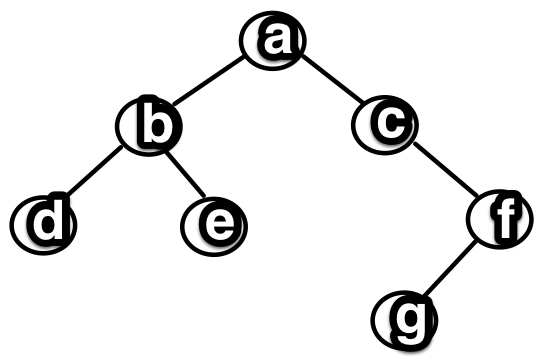
Gerçekleyeceğimiz binary tree sıralanabilen her türden veriyi saklayabiliyor olacak. Bu sebeple (type parametreleri kodu biraz karıştırsa da) generic olarak gerçekleyeceğiz. Açıklamalar kod içerisinde yorum satırları olarak yer alıyor.

// Tree için ayrı bir yapı bulunmuyor. 
abstract class Tree[+T <% Ordered[T]] {
  def insert[S >: T <% Ordered[S]](x: S): Tree[S]
}

// Her Node aynı zamanda bir Tree'dir. Node veriyi sakladığı gibi sol ve sağ Tree'lere referanslar da içerir.
case class Node[+T <% Ordered[T]](value: T, left: Tree[T], right: Tree[T]) extends Tree[T] {
  override def insert[S >: T <% Ordered[S]](x: S) =
    // Eklenecek veriye ağaç üzerinde uygun yer arıyoruz.
    if (x < value) Node(value, left.insert(x), right)
    else Node(value, left, right.insert(x))

  override def toString = "(" + left.toString() + "<-" + value + "->" + right.toString() + ")"
}

// Her Node mutlaka bir left ve right Tree'ye sahiptir. Ancak yaprak(leaf) düğümler için bu Tree'ler boş olabilir. 
// End yapısı ile bu durumu gerçekliyoruz.
case object End extends Tree[Nothing] {
  def insert[T <% Ordered[T]](x: T) = Node(x, End, End)
  override def toString = "."
}

Yukarıdaki resimdeki ağacı aşağıdaki kod ile oluşturabilecek durumdayız artık. toString metodunun çıktısı yine kod içinde görülüyor.

val tree = Node('a',
  Node('b', Node('d'), Node('e')),
  Node('c', End, Node('f', Node('g'), End)))

// (((.<-d->.)<-b->(.<-e->.))<-a->(.<-c->((.<-g->.)<-f->.)))

Aynı ağaca sırasıyla n ve m harflerini eklersek ağacın yeni durumu aşağıdaki gibi olur.

tree.insert('n').insert('m')
//(((.<-d->.)<-b->(.<-e->.))<-a->(.<-c->((.<-g->.)<-f->((.<-m->.)<-n->.))))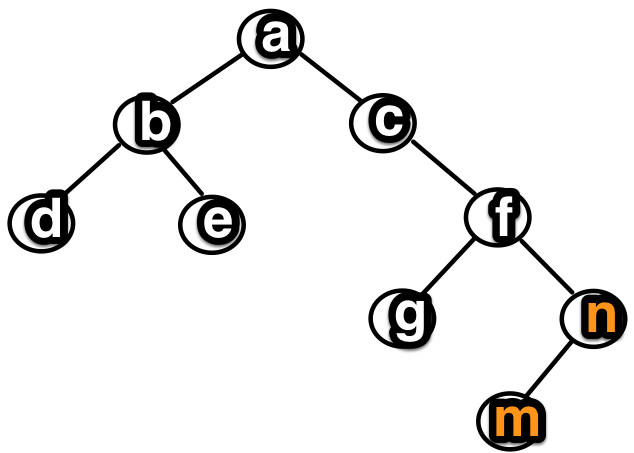

Resimden de anlaşıldığı üzere bu durumda ağacın dengesi hissedilir şekilde bozulmadı. Bir de aşağıdaki durumu değerlendirelim. Ağaca sırasıyla 1, 2, 5 ve 7 değerlerini ekleyelim.

Node(1).insert(2).insert(5).insert(7)
//(.<-1->(.<-2->(.<-5->(.<-7->.))))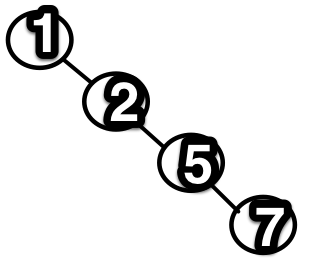

Resimde de göreceğiniz üzere ağacımız bu haliyle bir listeden farksız. Başka bir deyişle eğer veri kümesine artan değerler ekleniyorsa ağaçtan ancak bir liste kadar performans alabiliyoruz. Bu sebeple aşağıda bir Red-Black Tree gerçeklemesi paylaşıyorum. Kodun daha anlaşılır olması için type parametrelerini kaldırım. Bundan dolayı RedBlackTree yapısı yalnızca Int türünden veriler için çalışabiliyor.

Red-Black Tree algoritması için nette oldukça fazla kaynak var. Bu sebeple algoritmayı araştırmayı okuyuculara bırakıyorum. Kodun sonundaki örnekte ağaca sırasıyla 1, 2, 3, 4, 5 ve 6 değerleri ekleniyor. Ağacın yapısını aşağıdaki resimde paylaşıyorum. Yukarıdaki örneğe kıyasla ağacın nasıl da dengeli dağıldığında dikkat ediniz.

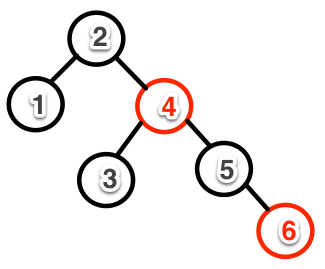
sealed trait Color
case object Red extends Color
case object Black extends Color

abstract class RedBlackTree {

  def blacken(n: RedBlackTree): RedBlackTree = {
    n match {
      case Leaf() => n
      case Tree(_, left, value, right) => Tree(Black, left, value, right)
    }
  }

  def balance(color: Color)(left: RedBlackTree)(value: Int)(right: RedBlackTree): RedBlackTree = {
    (color, left, value, right) match {
      case (Black, Tree(Red, Tree(Red, a, xV, b), yV, c), zV, d) => 
        Tree(Red, Tree(Black, a, xV, b), yV, Tree(Black, c, zV, d))

      case (Black, Tree(Red, a, xV, Tree(Red, b, yV, c)), zV, d) => 
        Tree(Red, Tree(Black, a, xV, b), yV, Tree(Black, c, zV, d))

      case (Black, a, xV, Tree(Red, Tree(Red, b, yV, c), zV, d)) => 
        Tree(Red, Tree(Black, a, xV, b), yV, Tree(Black, c, zV, d))

      case (Black, a, xV, Tree(Red, b, yV, Tree(Red, c, zV, d))) => 
        Tree(Red, Tree(Black, a, xV, b), yV, Tree(Black, c, zV, d))

      case (color, left, value, right) => 
        Tree(color, left, value, right)
    }
  }

  def modWith(value: Int): RedBlackTree

  def insert(value: Int) = blacken(modWith(value))
}

case class Leaf extends RedBlackTree {
  def modWith(value: Int): RedBlackTree = {
    Tree(Red, this, value, this)
  }
  override def toString = "."
}

case class Tree(color: Color, left: RedBlackTree, value: Int, right: RedBlackTree) extends RedBlackTree {
  def modWith(value: Int): RedBlackTree = {
    if (value < this.value) balance(color)(left.modWith(value))(this.value)(right)
    else if (value > this.value) balance(color)(left)(this.value)(right.modWith(value))
    else this
  }
  override def toString = 
    "(" + left.toString() + "<-" + value + "(" + color + ")->" + right.toString() + ")"
}

object RedBlackTree {
  def apply(args: Int*): RedBlackTree = {
    var tree: RedBlackTree = Leaf()
    for (value <- args) {
      tree = tree.insert(value)
    }
    tree
  }
}

RedBlackTree(1, 2, 3, 4, 5, 6)
//((.<-1(Black)->.)<-2(Black)->((.<-3(Black)->.)<-4(Red)->(.<-5(Black)->(.<-6(Red)->.))))

Follow me on Twitter